Permute 2 3 Download Free
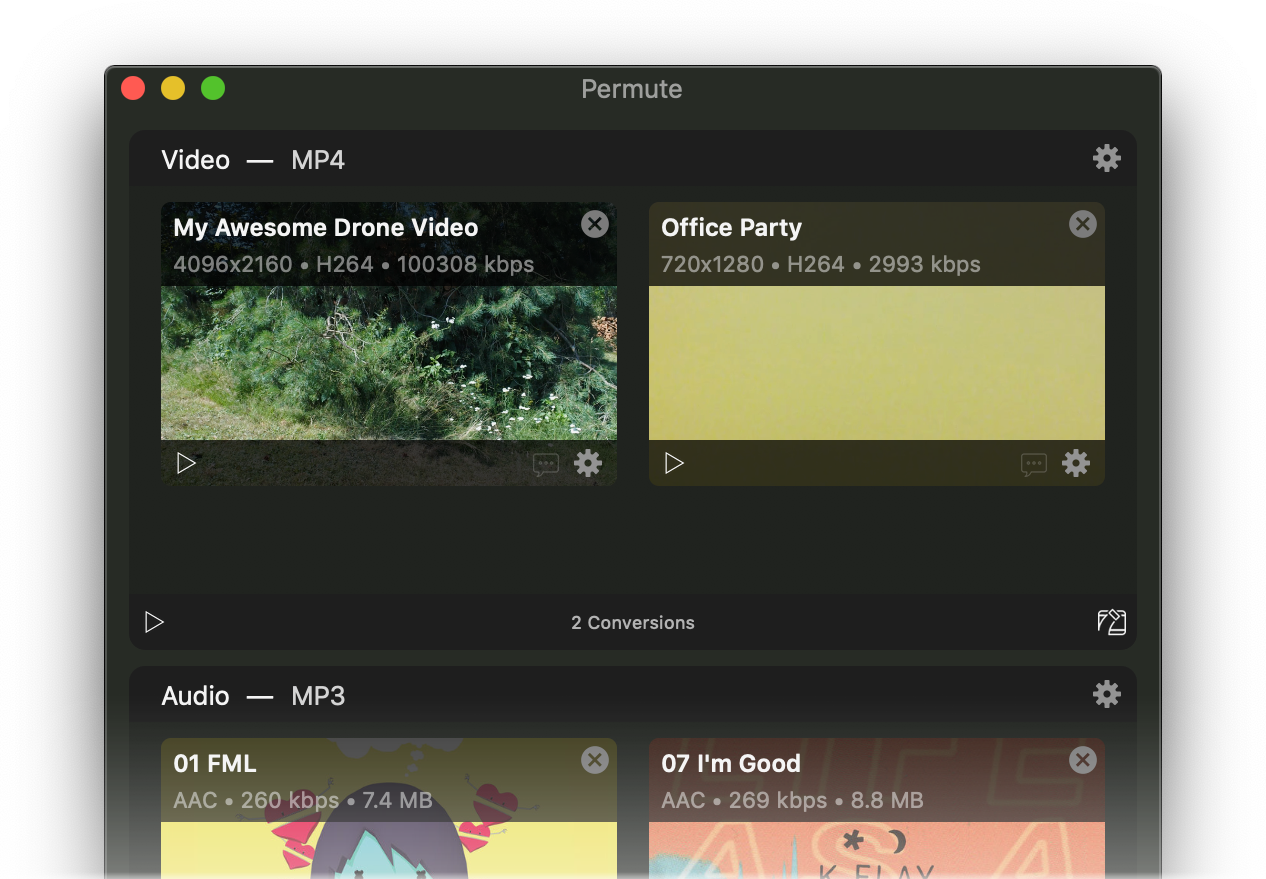
- Permute 3.2.7 Multilingual macOS 56 mb. Video, audio and image files come in many different kinds and shapes, but sometimes you need a specific format since your iPad or DVD player won't play that video. That is what Permute is for - easily convert your media files to various different formats.
- 1.3 Operating systems compatible with NCO. In its time on Earth, NCO has been successfully ported and tested on so many 32- and 64-bit platforms that if we did not write them down here we would forget their names: IBM AIX 4.x, 5.x, FreeBSD 4.x, GNU/Linux 2.x, LinuxPPC, LinuxAlpha, LinuxARM, LinuxSparc64, LinuxAMD64, SGI IRIX 5.x and 6.x, MacOS X 10.x, DEC OSF, NEC Super-UX 10.x, Sun SunOS 4.1.
Choose Download Address: Download 1 Download 2 Download 3 IExif supports for general JPEG image & EXIF templet file Additionally, if you need view EXIF info in TIFF image file, please choose Opanda IExifPro 2.3.
Math::Permute::Partitions - Generate all the permutations of a partitioned list.
Permute 2 3 Download Free Pc
Generate all the permutations of a partitioned list using the standard Perl metaphor.
permutePartitions() returns the number of permutations in both scalar and array context.
permutePartitions() is written in 100% Pure Perl.
The permutePartitions() function is exported.
Standard Module::Build process for building and installing modules:
10 Permute 3
Or, if you're on a platform (like DOS or Windows) that doesn't require the './' notation, you can do this:
PhilipRBrenan@appaapps.com
http://www.appaapps.com
Based on an idea from Philipp Rumpf
Copyright (c) 2015 Philip R Brenan.
This module is free software. It may be used, redistributed and/or modified under the same terms as Perl itself.
To install Math::Permute::Partitions, copy and paste the appropriate command in to your terminal.
For more information on module installation, please visit the detailed CPAN module installation guide.
Heap's algorithm generates all possible permutations of n objects. It was first proposed by B. R. Heap in 1963.[1] The algorithm minimizes movement: it generates each permutation from the previous one by interchanging a single pair of elements; the other n−2 elements are not disturbed. In a 1977 review of permutation-generating algorithms, Robert Sedgewick concluded that it was at that time the most effective algorithm for generating permutations by computer.[2]

The sequence of permutations of n objects generated by Heap's algorithm is the beginning of the sequence of permutations of n+1 objects. So there is one infinite sequence of permutations generated by Heap's algorithm (sequence A280318 in the OEIS).
Details of the algorithm[edit]
For a collection containing n different elements, Heap found a systematic method for choosing at each step a pair of elements to switch in order to produce every possible permutation of these elements exactly once.
Described recursively as a decrease and conquer method, Heap's algorithm operates at each step on the initial elements of the collection. Initially and thereafter . Each step generates the permutations that end with the same final elements. It does this by calling itself once with the element unaltered and then times with the () element exchanged for each of the initial elements. The recursive calls modify the initial elements and a rule is needed at each iteration to select which will be exchanged with the last. Heap's method says that this choice can be made by the parity of the number of elements operated on at this step. If is even, then the final element is iteratively exchanged with each element index. If is odd, the final element is always exchanged with the first.
Permute 2 3 Download Free Hidden Object Games
One can also write the algorithm in a non-recursive format.[3]
Proof[edit]
In this proof, we'll use the implementation below as Heap's Algorithm. While it is not optimal (see section below)[clarification needed], the implementation is nevertheless still correct and will produce all permutations. The reason for using the below implementation is that the analysis is easier, and certain patterns can be easily illustrated.
Claim: If array A has length n, then performing Heap's algorithm will either result in A being 'rotated' to the right by 1 (i.e. each element is shifted to the right with the last element occupying the first position) or result in A being unaltered, depending if n is even or odd, respectively.
Basis: The claim above trivially holds true for as Heap's algorithm will simply return A unaltered in order.
Induction: Assume the claim holds true for some . We will then need to handle two cases for : is even or odd.
If, for A, is even, then the subset of the first i elements will remain unaltered after performing Heap's Algorithm on the subarray, as assumed by the induction hypothesis. By performing Heap's Algorithm on the subarray and then performing the swapping operation, in the kth iteration of the for-loop, where , the kth element in A will be swapped into the last position of A which can be thought as a kind of 'buffer'. By swapping the 1st and last element, then swapping 2nd and last, all the way until the nth and last elements are swapped, the array will at last experience a rotation. To illustrate the above, look below for the case
If, for A, is odd, then the subset of the first i elements will be rotated after performing Heap's Algorithm on the first i elements. Notice that, after 1 iteration of the for-loop, when performing Heap's Algorithm on A, A is rotated to the right by 1. By the induction hypothesis, it is assumed that the first i elements will rotate. After this rotation, the first element of A will be swapped into the buffer which, when combined with the previous rotation operation, will in essence perform a rotation on the array. Perform this rotation operation n times, and the array will revert to its original state. This is illustrated below for the case .
The induction proof for the claim is now complete, which will now lead to why Heap's Algorithm creates all permutations of array A. Once again we will prove by induction the correctness of Heap's Algorithm.
Basis: Heap's Algorithm trivially permutes an array A of size 1 as outputting A is the one and only permutation of A.
Induction: Assume Heap's Algorithm permutes an array of size i. Using the results from the previous proof, every element of A will be in the 'buffer' once when the first i elements are permuted. Because permutations of an array can be made by altering some array A through the removal of an element x from A then tacking on x to each permutation of the altered array, it follows that Heap's Algorithm permutes an array of size , for the 'buffer' in essence holds the removed element, being tacked onto the permutations of the subarray of size i. Because each iteration of Heap's Algorithm has a different element of A occupying the buffer when the subarray is permuted, every permutation is generated as each element of A has a chance to be tacked onto the permutations of the array A without the buffer element.
Frequent mis-implementations[edit]
It is tempting to simplify the recursive version given above by reducing the instances of recursive calls. For example, as:
This implementation will succeed in producing all permutations but does not minimize movement. As the recursive call-stacks unwind, it results in additional swaps at each level. Half of these will be no-ops of and where but when is odd, it results in additional swaps of the with the element.
| swaps | additional = swaps | ||
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 |
| 3 | 5 | 6 | 1 |
| 4 | 23 | 27 | 4 |
| 5 | 119 | 140 | 21 |
| 6 | 719 | 845 | 126 |
| 7 | 5039 | 5922 | 883 |
| 8 | 40319 | 47383 | 7064 |
| 9 | 362879 | 426456 | 63577 |
These additional swaps significantly alter the order of the prefix elements.
The additional swaps can be avoided by either adding an additional recursive call before the loop and looping times (as above) or looping times and checking that is less than as in:
The choice is primarily aesthetic but the latter results in checking the value of twice as often.
See also[edit]
References[edit]
- ^Heap, B. R. (1963). 'Permutations by Interchanges'(PDF). The Computer Journal. 6 (3): 293–4. doi:10.1093/comjnl/6.3.293.
- ^Sedgewick, R. (1977). 'Permutation Generation Methods'. ACM Computing Surveys. 9 (2): 137–164. doi:10.1145/356689.356692.
- ^Sedgewick, Robert. 'a talk on Permutation Generation Algorithms'(PDF).